Communication

Claude E. Shannon and Warren Weaver developed The Mathematical Theory of Communication in 1948 to explain the way information was transmitted in the telecommunication industry. This theory provides a framework for analyzing the effectiveness of communication channels in transmitting information

It was developed to explain the way telephone cables and radio waves transmit a signal. This model of communications can be applied to the way in which Web site designers/owners (the information source) communicates to the site visitors (destination). The designer's job is to encode the site's message(s) and the visitor's to decode the message(s).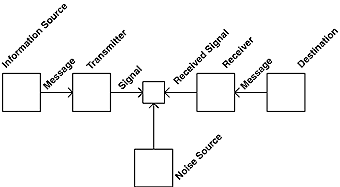

Shannon and Weaver defined three levels of communication problems with the following three questions:

• Technical - How accurately can the symbols of communication be transmitted?
• Semantic - How precisely do the transmitted symbols convey the desired meaning?
• Effectiveness - How effectively does the received meaning affect conduct in the desired way? [1]

• Is the Web icon visible enough?
   
• Is the Web icon understandable?
   
• Will the Web icon create the desired effect?

This theory has been applied to communication in general, but the paper is primarily about modulation and feedback of signals. The document contains many mathematical formulas that are applicable to signal-to-noise ratio. But communications scholars have generalized it to explain the sender-receiver relationship between individuals and in mass communication, not just between telecommunication devices. Claude Shannon's paper is available online as a pdf file.

"Communication is defined as the transfer of information from a source to a receiver. The goal of a communicator is to accomplish this process efficiently and effectively. Hence, communication theorists are committed to find and provide models by which communication can be enhanced. The challenge is to come up with the right combination of codes, media, and contexts in order to make the transfer of information fast, cost effective, and accurate. This process cannot be separated from the fact that humans are the ones that decode the information they receive through a particular medium in a specific context and make meaning out of it. This is where semiotics comes into play."[2]

Sources:

1. Mollerup, Per. Marks in Excellence,  pg. 68
2. Colón, Carlos, Communication Science vs. Semiotics,
   http://ezinfo.ucs.indiana.edu/~ccolon/Semiotics/ccolon1.html